記路

插入排序

思想

插入排序就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、数量加一的有序数据。它类似于玩扑克牌时的抓牌过程：每拿一张牌将其插入到手里排好序的牌中，使其保持有序。

插入算法把要排序的数组分成两部分：已排序部分、未排序部分。每一轮排序都是从未排序部分取出一个元素插入到已排序部分的合适位置，初始的已排序部分只有一个元素。由于插入排序发生在数组中，在找到合适的插入位置后，需要先移动该位置及之后的元素，将它腾出来放待插入元素。

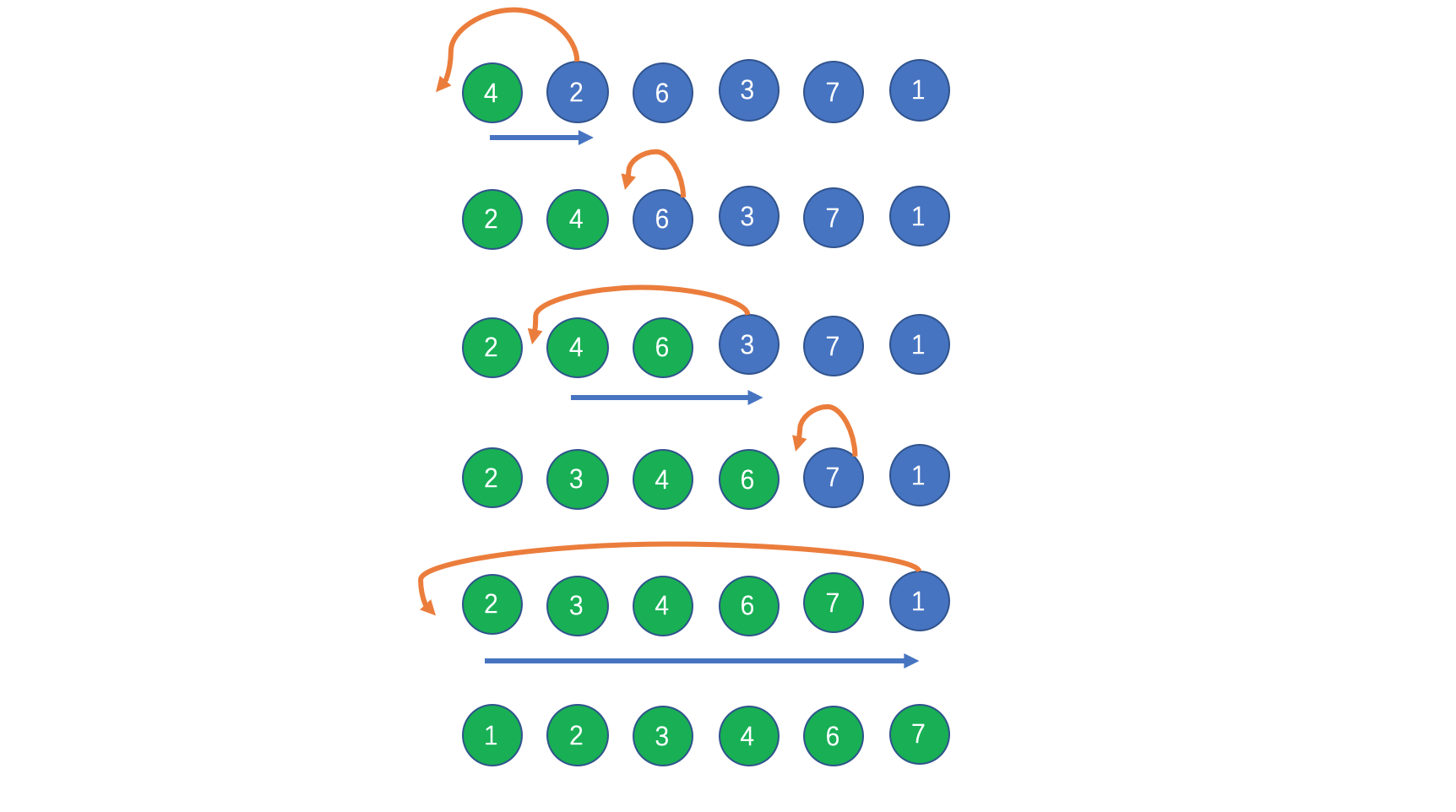
假设待排序数组为4, 2, 6, 3, 7, 1，它的排序过程为：
insert sort

分析

空间复杂度：排序过程不需要额外申请辅助空间，空间复杂度为O(1)
时间复杂度：
- 最好情况：完全正序时，不需要移动元素，每个元素分别和已排序部分最后元素进行一次比较，时间复杂度为O(n)
- 最差情况：完全逆序时，每次都需要将已排序部分的全部元素往后移动，以腾出第一个位置插入元素，时间复杂度为O(n^2)
- 平均情况：每次在已排序部分寻找合适的插入位置的平均时间复杂度为O(n)，进行n次循环，总体平均复杂度为O(n^2)
适用性：由于插入排序伴随着大量的数组元素移动，仅适用于少量数据的情况
稳定性：对于值相同的数据，可以选择将先出现的数据保持在后出现的数据之前，这样数据的前后顺序不变，插入排序是稳定排序

实现

# 插入排序
def insert_sort(lists):
	count = len(lists)
	
	for i in range(1, count):
		key = lists[i]
		j = i - 1
		while j >= 0:
			if lists[j] > key:
				lists[j + 1] = lists[j]
				lists[j] = key
				j -= 1
	 return lists

冒泡排序

思想

冒泡排序的基本思想是将元素进行两两比较，将较大（或者较小）的元素往右交换，每一轮排序结束后，最后的元素将是最大的那个。然后除了已经冒出来的最大元素，再重复进行刚刚的步骤。

分析

空间复杂度：排序过程不需要额外申请辅助空间，空间复杂度为O(1)
时间复杂度：
- 最好情况：完全正序时，只需要一轮循环进行两两比较，不需要交换，时间复杂度为O(n)
- 最差情况：完全逆序时，每轮循环都要把最左边的元素逐个交换到最右边，时间复杂度为O(n^2)
- 平均情况：每轮循环中，需要两两比较的平均复杂度为O(n)，因此总体平均时间复杂度为O(n^2)

实现

# 冒泡排序
def bubble_sort(lists):
	count = len(lists)
	for i in range(0, count):
		for j in range(i, count - i):
			if lists[j] > lists[i]:
				lists[i], lists[j] = lists[j], lists[i]
	return lists

直接选择排序

基本思想：第1趟，在待排序记录r1 ~ r[n]中选出最小的记录，将它与r1交换；第2趟，在待排序记录r2 ~ r[n]中选出最小的记录，将它与r2交换；以此类推，第i趟在待排序记录r[i] ~ r[n]中选出最小的记录，将它与r[i]交换，使有序序列不断增长直到全部排序完毕。

# 选择排序
def select_sort(lists):
	count = len(lists)
	for i in range(0, count):
		min = i
		for j in range(i + 1, count):
			if lists[min] > lists[j]:
				min = j
		lists[min], lists[i] = lists[i], lists[min]
return lists

归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

Python实现：

def merge(left, right):
	 i, j = 0, 0
	 result = []
	 while i < len(left) and j < len(right):
		if left[i] <= right[j]:
			result.append(left[i])
			i += 1
		 else:
			result.append(right[j])
			j += 1

	 result += left[i:]
	 result += right[j:]
	 return result


# 归并排序
def merge_sort(lists):
	if len(lists) <= 1:
		return lists
	num = len(lists) / 2
	left = merge_sort(lists[:num])
	right = merge_sort(lists[num:])
 return merge(left, right)

public class MergeSortMain {
	/**
	 * 归并所需要的辅助数组
	 */
	private static Comparable[] aux;
	public static void sort(Comparable[] array){
		aux= new Comparable[array.length]; //一次性分配空间
		sort(array, 0 ,array.length-1);
	}

	/**
	* 自底向上的归并
	* @param array
	*/
	public static void sort2(Comparable[] array){
		//进行lg(length)次两两归并
		int length = array.length;
		aux = new Comparable[length];
		for (int sz=1; sz < length; sz=sz+sz){
			for (int low = 0; low < length-sz; low += sz+sz){
				merge(array,low,low+sz-1,Math.min(low+sz+sz-1,length-1));
			}
		}
	}
	/**
	 * 自顶向下的归并排序，分治，基于原地归并做的递归
	 * @param array
	 * @param low
	 * @param high
	 */
	private static void sort(Comparable[] array, int low, int high){
		if(high < low)
			return;
		int mid = low +(high-low)/2;
		sort(array, low, mid);
		sort(array, mid+1, high);
		merge(array, low, mid, high);
	 }

	/**
	  * 原地归并的抽象方法
	  * 将涉及的所有元素复制到一个辅助数组中，再把归并的结果放回原数组中
	  * @param orignialArray
	  * @param low
	  * @param mid
	  * @param high
	  */
	private static void merge(Comparable[] orignialArray, int low, int mid, int high) {
	  // 将a[low..mid]和a[mid+1..high]归并
		int i = low, j = mid+1;
		for (int k = low; k<=high ;k++){// 将orignialArray[low..high]复制到aux[low..high]
			aux[k] = orignialArray[k];
		}
		for (int k = low; k<=high; k++){//归并回到originalArray[low..high]
			if (i > mid){//左边的数组元素已经全部放进去了
				orignialArray[k] = aux[j++];
		   } else if (j > high){//右边的数组元素已经全部放进去了
				orignialArray[k] = aux[i++];
		   } else if (isLess(aux[j], aux[i])){//如果第j个数比第i个数小，则把第j个数放进数组，j加1
				orignialArray[k] = aux[j++];
	   } else {//如果第i个数比第j个数小，则把第i个数放进数组，i加1
			orignialArray[k] = aux[i++];
	   }
	}
}

	private static boolean isLess(Comparable i, Comparable j) {
		return i.compareTo(j) < 0;
	}
}

記路

算法 - 排序

插入排序

思想

分析

实现

冒泡排序

思想

分析

实现

直接选择排序

归并排序

HBase

void指针